圆锥曲线常规思路之计算
在我刚从事数学教学的时候加了一个 QQ 群,里面介绍各种各样的秒杀公式等,刚开始还是很好奇的,后来没过多久就退群了,个人觉得此教法并不健康,有的连老师本人都无法搞定更何况学生呢?光记住结论不晓得来由是万万不值得推崇的,我们就拿圆锥曲线的硬解定理来说,一起看下:
1、 若曲线 \frac{x^2}{m}+\frac{y^2}{n}=1 与 Ax+By+C=0 相交于 E,F 两点,则
x _ { 1 } + x _ { 2 } = \frac { - 2 A C m } { \varepsilon} , x _ { 1 } x _ { 2 } = \frac { m ( C ^ { 2 } - B ^ { 2 } n ) } { \varepsilon } , \Delta^ { \prime } = m n (\varepsilon - C ^ { 2 } ) , | E F | = \frac { 2 \sqrt { ( A ^ { 2 } + B ^ { 2 } )\Delta ^ { \prime } } } { | \varepsilon| } ,其中 \varepsilon= A ^ { 2 } m + B ^ { 2 } n , \Delta ^ { \prime } = \frac { 1 } { 4 B ^ { 2 } } \Delta
要是学生,你敢背这?怕是不行的,万一错了一个,就是满盘皆输。之所以有的什么秒杀群会出现这个是因为正中了些不愿意计算的学生的口味,接下来的篇幅我们一起来算算看常规的直线与曲线联立的题目的解法,就不纯粹使用字母了,我们带一些数字看看
2、 若椭圆\frac{x^2}{4}+y^2=1与 y=k(x-1)+2 相交于 A,B 两点
先联立 \begin{cases} & \frac { x ^ { 2 } } { 4 ^ { 2 } } + y ^ { 2 } = 1① \\ & y = k ( x - 1 ) + 2 ② \end{cases} ,可以先将①式化成 x²+4y²=4 ,然后再把②式带入,要不然带入之后会有分数的形式,比较难看也比较难算,得 x²+4[k(x-1)+2]²=4 ,中括号里面的 k(x-1)+2 中 k(x-1) 看成一个整体,然后完全平方计算,如果你给改成 kx-k+2 在平方计算的话比较难算,容易出错 x²+4[k²(x-1)²+4+4k(x-1)]-4=0\Rightarrow x²+4[k²(x²+1-2x)+4+4k(x-1)]-4=0\Rightarrow x²+4[k²x²+k²-2k²x+4+4kx-4k]-4=0\Rightarrow x²+4k²x²+4k²-8k²x+16+16kx-16k-4=0
最后就是合并一下,得 (4k²+1)x²+(16k-8k²)x+4k²-16k+12=0 ,到这里先别忙着什么韦达定理之类的操作,在此之前我们还是需要先搞一下判别是,即 ∆=(16k-8k²)²-4(4k²+1)(4k²-16k+12) =256k²+64k4-256k³-4(16k4-64k³+48k²+4k²-16k+12) =256k²+64k4-256k³-4(16k4-64k³+52k²-16k+12) =256k²+64k4-256k³-64k4+256k³-208k²+64k-48 =48k²+64k-48 ,因为直线与椭圆有两个交点,所以可以得到 ∆>0⇒48k²+64k-48>0 .
首先看看能不能十字相乘,如果不能那就使用求根公式看看,得 k \lt \frac { - 2 - \sqrt { 13 } } { 3 } , k \gt \frac { - 2 + \sqrt { 13 } } { 3 } .
这里注意一下:题目说有交点,再加上直线 y=k(x-1)+2 所过定点 (1,2) 在椭圆外,所以我们可以得出 k 的取值范围。但是有的学生在做此类题目的时候发现有的 ∆>0 是恒成立的,是怎么回事呢?原因就在于直线所过的那个定点在不在椭圆内,我们打个比方
3、 若椭圆\frac{x^2}{4}+y^2=1与 y=k(x-1) 相交于 A,B 两点
先联立\begin{cases} & \frac { x ^ { 2 } } { 4 ^ { 2 } } + y ^ { 2 } = 1 \\ & y = k ( x - 1 ) \end{cases} ,得 (4k²+1)x²-8k²x+4k²-4=0\Rightarrow ∆=(-8k²)²-4(4k²-4)(4k²+1) =60k²+16>0
这时候就是恒成立的,因为过定点的那条直线肯定与椭圆有两个交点啊,过椭圆外一定点的直线就不一定了,很简单的道理。

我们回到例题 2 ,在经过判别式之后就可以写出韦达定理的式子了,在此前(也就是 2020 年的六月份之前)一般是不给直接使用的,而是通过求根公式,然后相加或者乘来得到韦达式子的。
x _ { 1 } + x _ { 2 } = - \frac { 16 k - 8 k ^ { 2 } } { 4 k ^ { 2 } + 1 } , x _ { 1 } x_{2}= \frac { 4 k ^ { 2 } - 16 k + 12 } { 4 k ^ { 2 } + 1 }
关于求根公式与韦达定理推导,我们写上简单的证明
ax²+bx+c=0(a≠0)
判别式,初中数学上面(苏科版)关于判别式只是说是 b²-4ac ,并没有说用 ∆ 这个符号来表示,那这里为方便,就直接用 ∆=b²-4ac 来表示判别式了。接下来一起来推导一下:
首先是配方,得 ( x + \frac { b } { 2 a } ) ^ { 2 } = \frac { b ^ { 2 } - 4 a c } { 4 a ^ { 2 } } ( a \neq 0 )
(1)当 Δ>0 时,方程有两个不相等的实数根 x _ { 1,2 } = \frac { - b \pm \sqrt { b ^ { 2 } - 4 a c } } { 2 a }
(2) 当 Δ=0 时,方程有两个相等的实数根 x _ { 1 } = x _ { 2 } = - \frac { b } { 2 a }
(3) 当 Δ<0 时,方程没有实数根.
这个韦达定理肯定是方程有解的时候才会用的,我们这里就以 Δ>0 时来演示一下:
x _ { 1 } = \frac { - b - \sqrt { b ^ { 2 } - 4 a c } } { 2 a } , x _ { 2 } = \frac { - b + \sqrt { b ^ { 2 } - 4 a c } } { 2 a }
x _ { 1 } + x _ { 2 } = \frac { - b - \sqrt { b ^ { 2 } - 4 a c } } { 2 a } + \frac { - b + \sqrt { b ^ { 2 } - 4 a c } } { 2 a } = - \frac { 2 b } { 2 a } = - \frac { b } { a }
x _ { 1 } \cdot x _ { 2 } = \frac { - b - \sqrt { b ^ { 2 } - 4 a c } } { 2 a } \cdot \frac { - b + \sqrt { b ^ { 2 } - 4 a c } } { 2 a } = \frac { b ^ { 2 } - b ^ { 2 } + 4 a c } { 4 a ^ { 2 } } = \frac { c } { a }
即得 x _ { 1 } + x _ { 2 } = - \frac { b } { a } , x _ { 1 } \cdot x _ { 2 } = \frac { c } { a }
这时候我们先列出一个问题
4、 若椭圆\frac{x^2}{4}+y^2=1与 y=k(x-1)+2 相交于 A,B 两点, OA \bot OB ,求 k 的值
圆锥曲线当中遇到垂直,一般会得出两个有用的条件,分别是利用向量 \vec{OA}\bot\vec{OB}\Rightarrow x _ { 1 } x _ { 2 } + y _ { 1 } y_{2}= 0 以及 O A \bot O B \Rightarrow k _ { 1 } k _ { 2 } = - 1 .
这里我们用第一个,设 A(x_{1},y_{1}),B(x_{2},y_{2}) ,因为\vec{OA}\bot\vec{OB}\Rightarrow x _ { 1 } x _ { 2 } + y _ { 1 } y_{2}= 0,那这里的 y_{1}y_{2} 怎么办?我们就把它转化为 x_{1},x_{2}⇒ \begin{cases}&y _ { 1 } = k ( x _ { 1 } - 1 ) + 2 \\&y _ { 2 } = k ( x _ { 2 } - 1 ) + 2 \end{cases}\Rightarrow y _ { 1 } y_{2}=[k(x_{1}-1)+2][k(x_{2}-1)+2]= k²x_{1}x_{2}+(2k-k²)(x_{1}+x_{2})+k²-4k+4=0
所以可以得到 x _ { 1 } x _ { 2 } + y _ { 1 } y_{2}= (k²+1)x_{1}x_{2}+(2k-k²)(x_{1}+x_{2})+k²-4k+4=0 ,此时我们只要把 x _ { 1 } + x _ { 2 } = - \frac { 16 k - 8 k ^ { 2 } } { 4 k ^ { 2 } + 1 } , x _ { 1 }x_{2} = \frac { 4 k ^ { 2 } - 16 k + 12 } { 4 k ^ { 2 } + 1 } 带进去就行了,得 ( k ^ { 2 } + 1 ) \frac { 4 k ^ { 2 } - 16 k + 12 } { 4 k ^ { 2 } + 1 } + ( 2 k - k ^ { 2 } ) ( - \frac { 16 k - 8 k ^ { 2 } } { 4 k ^ { 2 } + 1 } ) + k ^ { 2 } - 4 k + 4 = 0 ,通分 \frac { ( k ^ { 2 } + 1 ) ( 4 k ^ { 2 } - 16 k + 12 ) } { 4 k ^ { 2 } + 1 } - \frac { ( 2 k - k ^ { 2 } ) ( 16 k - 8 k ^ { 2 } ) } { 4 k ^ { 2 } + 1 } + \frac { ( 4 k ^ { 2 } + 1 ) ( k ^ { 2 } - 4 k + 4 ) } { 4 k ^ { 2 } + 1 } = 0 ,化简 k²-20k+16=0 ,解得 x=10±2\sqrt{21}
考虑到k的取值范围,两个结果都是对的(一般都是对的).
5、 若椭圆\frac{x^2}{4}+y^2=1与 y=k(x-1)+2 相交于 A,B 两点,求弦长 AB 表示
这个呢就用到弦长公式,学生们要记住两个公式 \begin{cases}&A B = \sqrt { 1 + k ^ { 2 } } | x _ { 1 } - x _ { 2 } | \\&A B = \sqrt { 1 + \frac { 1 } { k ^ { 2 } } } | y _ { 1 } - y _ { 2 } |\end{cases}
首先我们要知道这个弦长公式到底是怎么推导出来的,为什么是这样子。先从两点之间的距离公式算起
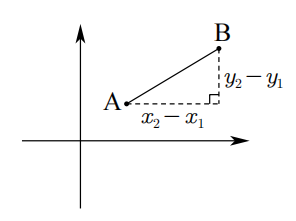
则 A B = \sqrt { ( x _ { 2 } - x _ { 1 } ) ^ { 2 } + ( y _ { 2 } - y _ { 1 } ) ^ { 2 } } ,然后带入所在的直线方程,即 A B = \sqrt { ( x _ { 2 } - x _ { 1 } ) ^ { 2 } + ( y _ { 2 } - y _ { 1 } ) ^ { 2 } } = \sqrt { ( x _ { 2 } - x _ { 1 } ) ^ { 2 } + [ ( k ( x _ { 1 } - 1 ) + 2 ) - ( k ( x _ { 2 } - 1 ) + 2 ) ] ^ { 2 } } = \sqrt { ( x _ { 2 } - x _ { 1 } ) ^ { 2 } + ( k x _ { 1 } - k x _ { 2 } ) ^ { 2 } } = \sqrt { ( x _ { 2 } - x _ { 1 } ) ^ { 2 } + k ^ { 2 } ( x _ { 1 } - x _ { 2 } ) ^ { 2 } } = \sqrt { ( 1 + k ^ { 2 } ) ( x _ { 1 } - x _ { 2 } ) ^ { 2 } } = \sqrt { 1 + k ^ { 2 } } | x _ { 1 } - x _ { 2 } |
关于上面的比较重要的还得是求 | x _ { 1 } - x _ { 2 } | ,即两根之差的绝对值,初升高小检测考到的次数还是蛮多的,自然也就有了以下的小结论: | x _ { 1 } - x _ { 2 } | = \sqrt { ( x _ { 1 } - x _ { 2 } ) ^ { 2 } } = \sqrt { x _ { 1 } ^ { 2 } - 2 x _ { 1 } x _ { 2 } + x _ { 2 } ^ { 2 } } = \sqrt { ( x _ { 1 } + x _ { 2 } ) ^ { 2 } - 4 x _ { 2 } } = \sqrt { ( - \frac { b } { a } ) ^ { 2 } - \frac { 4 c } { a } } = \sqrt { \frac { b ^ { 2 } - 4 a c } { a ^ { 2 } } } = \frac { \sqrt { b ^ { 2 } - 4 a c } } { | a | } = \frac { \sqrt { \Delta } } { | a | }
结论可以这么写:如果 x_{1} 和 x_{2} 分别是一元二次方程 ax²+bx+c=0(a≠0) 的两个根(即 Δ≥0 ),那么 | x _ { 1 } - x _ { 2 } | = \frac { \sqrt { \Delta } } { | a | }
好了,了解了这么多前提小知识,现在我们可以求解了 A B = \sqrt { 1 + k ^ { 2 } } | x _ { 1 } - x _ { 2 } | ,因此此时 | x _ { 1 } - x _ { 2 } | = \frac { \sqrt { \Delta} } { | a | } = \frac { \sqrt { 48 k ^ { 2 } + 64 k - 48 } } { 4 k ^ { 2 } + 1 } ,即 A B = \sqrt { 1 + k ^ { 2 } } \frac { \sqrt { 48 k ^ { 2 } + 64 k - 48 } } { 4 k ^ { 2 } + 1 } .
6、 若椭圆\frac{x^2}{4}+y^2=1与 y=k(x-1)+2 相交于 A,B 两点,求 \Delta OAB 面积最值
常规情况计算面积就是边与其高的乘积的一半,这里边就是弦长 AB ,高就是点到直线的距离,弦长公式我们已经推到过了,现在就是点到直线的距离公式该怎么推导了,即点 P(x_{0},y_{0}) 到直线 l:Ax+By+C=0 的距离 d = \frac { | Ax _ { 0 } + By _ { 0 } + C | } { \sqrt { A ^ { 2 } +B ^ { 2 } } }

首先是联立,两个式子,一个是两直线垂直,一个是点 H 在直线 l 上,所以有\begin{cases}&Ax+By+C=0 \\&\frac { y _ { 0 } - y } { x _ { 0 } - x } \cdot ( - \frac { A } { B } ) = - 1\end{cases} \Rightarrow ( A ^ { 2 } + B ^ { 2 } ) [ ( x _ { 0 } - x ) ^ { 2 } + ( y _ { 0 } - y ) ^ { 2 } ] = ( A x _ { 0 } + B y _ { 0 } + C ) ^ { 2 } \Rightarrow d = \sqrt { ( x _ { 0 } - x ) ^ { 2 } + ( y _ { 0 } - y ) ^ { 2 } } = \frac { | A x _ { 0 } + B y_ { 0 } + C | } { \sqrt { A ^ { 2 } + B ^ { 2 } } } ,这个书上有公式的,所以在这边只是简单的推导了一下,有兴趣的可以自行做做。
本题点到直线的距离计算是 d=\frac{\left| 2-k \right|}{\sqrt{1+k^2}} ,弦长 AB=\sqrt{1+k^2}\frac{\sqrt{48k^2+64k-48}}{4k^2+1} ,所以 S _ { \Delta OA B } = \frac { 1 } { 2 } A B \cdot d = \frac { | 2 - k | } { \sqrt { 1 + k ^ { 2 } } } \sqrt { 1 + k ^ { 2 } } \frac { \sqrt { 48 k ^ { 2 } + 64 k - 48 } } { 4 k ^ { 2 } + 1 } = \frac { | 2 - k | \sqrt { 48 k ^ { 2 } + 64 k - 48 } } { 4 k ^ { 2 } + 1 } = 4 \sqrt { \frac { ( k - 2 ) ^ { 2 } ( 3 k ^ { 2 } + 4 k - 3 ) } { ( 4 k ^ { 2 } + 1 ) ^ { 2 } } }
这个式子当初设置的时候应该是数字没有搞好,这里我们就当得到下面的式子看看(假设 k≥1 ),如下
S_{\Delta OAB}= \sqrt { 1 + k ^ { 2 } } \sqrt { ( \frac { - 12 k ^ { 2 } } { 1 + 3 k ^ { 2 } } ) ^ { 2 } - \frac { 4 (12k²-6) } { 1 + 3 k ^ { 2 } } } = \sqrt { 1 + k ^ { 2 } } \sqrt { ( \frac { - 12 k ^ { 2 } } { 1 + 3 k ^ { 2 } } ) ^ { 2 } - \frac { 4 ( 36 k ^ { 4 } - 6 k ^ { 2 } - 6 ) } { ( 1 + 3 k ^ { 2 } ) ^ { 2 } } } = \sqrt { 1 + k ^ { 2 } } \sqrt { \frac { 24 k ^ { 2 } + 24 } { ( 1 + 3 k ^ { 2 } ) ^ { 2 } } } = \frac { 2 \sqrt { 6 } ( 1 + k ^ { 2 } ) } { 1 + 3 k ^ { 2 } } = 2 \sqrt { 6 } \frac { \frac { 1 } { 3 } ( 1 + 3 k ^ { 2 } ) + \frac { 2 } { 3 } } { 1 + 3 k ^ { 2 } } = 2 \sqrt { 6 } ( \frac { 1 } { 3 } + \frac { 2 } { 9 k ^ { 2 } + 3 } )
因为 k≥1⇒9k²+3≥12⇒ \frac { 2 } { 9 k ^ { 2 } + 3 } \leq \frac { 1 } { 6 } \Rightarrow \frac { 1 } { 3 } + \frac { 2 } { 9 k ^ { 2 } + 3 } \leq \frac { 1 } { 2 } ,所以 2 \sqrt { 6 } ( \frac { 1 } { 3 } + \frac { 2 } { 9 k ^ { 2 } + 3 } ) \leq \sqrt { 6 } ,所以 S_{\Delta OAB} 面积的最大值是 \sqrt{6}
好了,此类题目的常规计算就到这边,当然还有其它的计算类型,我们之后慢慢拓展着讲。本节课里面的题目设置的数字比较随意,有的算不出什么结果(就比如例题 6 )或者说比较难算具体值等我都做了少许的"变样",以便能够算到最后。
以下我们总结一下本篇文章涉及到的知识点
圆锥曲线的硬解定理⇒不要背
判别式作用⇒掌握
求根公式推导⇒背上公式就行
韦达定理推导⇒背上公式就行
向量垂直⇒掌握
两直线垂直⇒掌握
弦长公式推导⇒掌握(公式就行)
两根差结论推导⇒掌握
分离常数⇒掌握
点到直线的距离公式推导⇒背上公式就行
本篇文章就到这边,有兴趣的一定自己演算一遍。
有需要文档的留言一下,我看人多不多,多的话我就直接贴到文章末尾自己自行下载了

