多面体编译领域的Feautrier调度算法是什么?
谢邀。我会在本文完整且系统地介绍多面体编译领域非常经典的Feautrier调度算法[1]。
虽然这是一篇1992年的上古论文,但即使是2008年另一篇多面体领域同样经典的PLUTO论文[2],在方法层面跟它相比也仅能算是“微小”的改进。如果读过了Feautrier的论文,我敢打赌,无论是FCO Placements[3],还是PLUTO,里面用到的方法不会有任何能再令我们感到新奇的东西。
这种时隔30年,idea也没有随着时间的流逝而变得过时的经典论文,可以帮助我们建立自己的思维框架,形成自己的思考,我觉得我们都应该好好学习一下!这也是我决定写这篇解读文章的初衷。
虽然我先前写过两篇介绍多面体的文章《零基础入门PLUTO的自动循环变换算法》和《零基础入门多面体编译的FCO Placements》:(因为我先学的是这两篇),但是本文还是会重新陈述一遍Feautrier调度算法所需要的理论框架,不要求读者事先掌握其他多面体的知识(学习92年的论文应该也不需要读过04年和08年的论文),力图让本文作为可以零基础入门多面体时的【第一篇】辅助材料来阅读。
本文的特点是采用了民科视角,重sense轻数学推导。我会试图解释清楚我们为什么要引入这个数学工具,它能解决什么问题,然后把求解的过程都交由isl软件去计算,而不是这个数学工具的本身是什么。
另外为了致敬我多面体学习时的启蒙论文Gri04,我决定采用同样的行文结构,采用非常多的章节,用层层递进的逻辑串联起本文,其中每个章节只讨论清楚一个足够小的主题,这样我觉得大家读起来也会比较轻松。

一、Feautrier调度算法的求解目标
一个程序可以由一组存在执行先后执行顺序限制(procedence constraints)的操作(operations)来表示,operations的集合为Ω,作用在Ω上由procedence constraints所表示的二元关系为Γ。
相比于PDG静态依赖图用静态语句之间的有向边抽象表示出多个动态实例之间的依赖关系,<Ω, Γ>构成动态的依赖图,能够表示出程序执行过程中所有操作之间每一个具体存在的依赖关系。
一个调度(schedule)为每一个操作赋予一个逻辑的执行时间(logical execution time),称为epoch。规定epoch较小值的操作没有执行完成以前,拥有更大epoch的操作不可以被执行。于是一个不违反procedence constraints的合法调度θ需要满足的充要条件(casuality condition)如下所示。
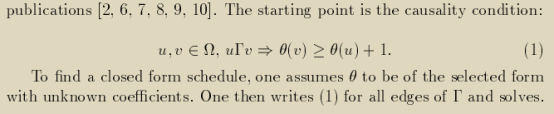
满足casuality condition且经过“优化的”调度θ即为我们最终求解的目标。
二、调度θ的宏观优化目标
根据程序依赖的固有特性,procedence constraints表示的二元偏序关系Γ具有传递性,进而可以构建Γ的传递闭包Γ*。
如果u, v∈Ω,在Γ*上却没有<u, v>或<v, u>的二元关系的话,那么这两个operations可以并行执行——我们对程序性能的优化在于挖掘笛卡尔积Ω×Ω中在偏序关系集合Γ*中不存在的元素对,它们是可以并行的。
调度θ也可以理解为二元关系:由casuality condition,uΓv => θ(u) < θ(v),存在θ上小于关系的元素对也具有Γ的关系。即,Γ是θ的子集——合法的θ一定蕴含Γ的关系,却也可能包含一些不必要的关系和多余的信息。
例如,本来可以并行的两个operations u和v也存在θ(u) < θ(v)的关系,那么它们在该调度下便不能并行执行了;也可能两个operations本来相继执行就可以保证程序正确,却间隔了很久很久。
一个“优化的”调度应当使得θ可以尽量接近Γ——这就是调度θ的宏观优化目标。
实际中考虑到θ求解的可行性,我们会设定更具体的criterion来替代笼统的宏观目标,尽管我们后面会看到某些情况求得的解跟宏观目标下的最优解可能存在一些差距。
三、程序通过Feautrier调度算法可以获得的优化
拥有相同θ值的不同operations可以同时执行,这也就是我们在当前逻辑时间下可以获得的并行度。
一个合法调度θ的最大值L被称为该调度下系统的执行时间。
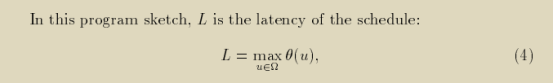
用系统所包含的operations的总数Card Ω的量级除以L的量级,可以得到系统平均可以获得的并行度。
用系统平均可获得的并行度的特征作为优化目标的criterion似乎值得考虑,在后面的第18-24小节里,我们会介绍三种更易求解的criterion,毕竟max(Card Ω/maxθ(u))似乎不太好求。
四、Feautrier调度算法似乎不讨论涉及代码生成的问题
将拥有相同θ值为t的operations组成一个集合F(t),称为front,用doall表示它们可以同时执行。
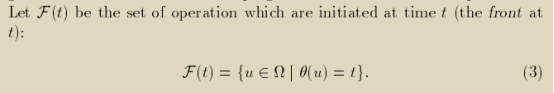
于是根据一个合法的调度θ,可以计算出F(t)包含的操作集合,并得到一个很trivial的代码生成。它描述了t从0-L的逻辑时间区间内,相同t值的F(t)集合并行执行,并由barrier屏障来保证不同的F(t)集合按t值从小到大的顺序依次执行。

不过,这种平凡的代码生成方式只是描述了operations之间的执行顺序,并不能保证我们能生成code size不会膨胀的代码。究竟是把F(t)里的每个operation实例进行展开,还是用卫函数(offending instructions)结合循环嵌套的方式进行代码生成?面向SMP处理器与面向systolic arrays的代码生成又有什么异同?这些在论文的Part I里并没有介绍,所以我打算再学习一些其他的文献以后写一篇关于polyscan的文章来讨论这个问题。
五、Feautrier调度算法的适用条件使得只能求得sub-optimal解,请大家随遇而安
为了能将θ的求解归约(reduce)为一个参数的整数线性规划问题(parametric linear program)用已知的LP工具来进行求解,我们令operations由用语句命名的迭代空间(iteration domain)上的整数迭代向量(integer iteration vector)表示,令procedence constraints只能由iteration vector上的仿射关系来表示(affine relations),最终待求的调度也必须是关于iteration vector的分段仿射函数(piecewise affine functions)的形式——后面在第23小节中我们再来解释它为什么可以是分段的。
如下所示,我们求解时为每个语句设定θ为仿射调度的形式(an affine scheduling of the form),未知系数为τ和α,每个语句不同的operations共享这组系数,然后设法优化求解。
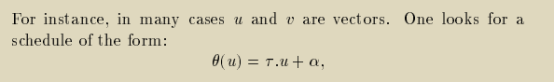
调度函数当然也可以不是仿射的,但可能求不出来。为了可以求解,我们限定的这类仿射调度函数θ是诸多Ω -> N函数的一个子集,我们在一个解空间的子集上搜索,能得到的也只是sub-optimal的解;即使没有求得解,也只意味着没有仿射解,但可能存在其他我们不知道的非仿射解。但这也没有办法,受限于数学工具的限制,我们只能尽可能接近最优解却很难达到最优解。
另一点sub-optimal的体现是,我们整数线性规划求解工具也是在整数空间上搜索未知系数的解,尽管未知系数也可以是实数。
六、调度时间的维度:one-dimension or multi-dimensions?
到目前为止我们其实并没有限制θ时间函数是一个一维函数。
如果认为第1小节中的θ(u)函数可以与一个标量1相加——比如一个小时可以+1s、以及多维向量可以用字典序(lexicographic order)进行大小的比较;认为第四节的θ(u) = t和do t = 0, L中的t和L也都是多维向量,这些也都没有什么是不可以的。
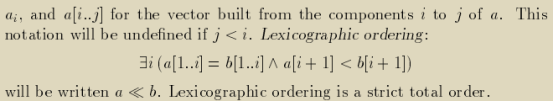
我们对程序的依赖图抽象、优化目标的设定与求解、最终的代码生成都可以轻松地从一维调度时间扩展到多维的调度时间上。
事实上正是因为并不是所有满足SCoP约束的程序都能有一个满足所有casuality condition的一维时间调度的解,我们才需要多维的调度时间,下图就是一个示例。

本例中因为存在迭代语句s = s + xxx,相邻的operations之间关于s都存在RAW依赖。故可以将存在procedence constraints的operations串联起来的ordering chain最短也要有O(n^2)的量级,ordering chain上的每一个operation都需要被分配一个不同逻辑时间。而一维的仿射逻辑时间最多能提供的数量级是O(n),是线性的,无法提供ordering chain所需的数量级。矛盾。
然而受限于篇幅的限制,本篇作为前篇只介绍一维时间的求解,当遇到上述仅仅一维的逻辑时间无法满足程序所有procedence constraints所构成的casuality condition的情况时直接报错,在后篇中我们再介绍如何求解多维时间满足上述情形。
七、我们需要compress infinite inequality of casuality condition
我们在第5小节中已经构建了仿射调度的形式θ(u) =τ*u+α,然后我们需要针对每一个程序中存在的procedence constraints:uΓv,去建立关于casuality condition的不等式约束:θ(v) - θ(u) - 1≥0。
然而如果我们考虑每一个具体的依赖关系的话,在一个存在结构参数n(structure parameters)的程序中可以存在无数个依赖,构建[infinite] inequality of casuality condition并在约束下求最优解是很困难的事。
八、如何compress inequality?How about the Vertex Method?
不妨先考虑一个更简单的问题。
我们对θ(u)其实有一个implicit的设定是其大于等于0。即,epoch是非负的。
那么对于一个domain D1为{ i : 0≤i≤n }的语句1的operations来说,如果设定调度的形式为:θ1(i) =τ*i+α的话,具体考虑每一个operation关于θ1(i)≥0的约束的话,最终我们会得到n+1个不等式:τ*0+α≥0,τ*1+α≥0,...,τ*n+α≥0。
我们想减少这些不等式的个数。

学过小学数学的人应该都知道,关于θ1(i) =τ*i+α仿射函数的极值点只能存在于线段的两个端点处。
于是我们只考虑边界上的点,来代替考虑整个线段上所有的点,可以将n+1个不等式compress成仅仅2个不等式:τ*0+α≥0和τ*n+α≥0,使得约束的规模不会随着程序迭代执行operations的规模增大而膨胀,使得调度θ的求解变得可行。
更正式地表述由上述sense得出的结论:根据多面体表示的对偶形式,在多面体内的所有点都满足某linear inequality≥0的充要条件是在由该多面体的convex hull生成的extremal points(vertices)上该linear inequality≥0也成立。
于是,如下所示,我们可以得出应用Vertex Method求解的算法框架将infinite inequality退化成finite set of linear inequality,使求解变得可能。

九、Farkas Lemma相比于Vertex Method能进一步compress inequality
虽然Vertex Method可以用多面体extremal points上需要满足的linear inequality来替代多面体内部所有点都需要满足的linear inequality,大大地减少了系统需要满足的linear inequality的数量,然而多面体实际上是由多个超平面相交来表示的,而不是由这些顶点来表示的。
从多面体的超平面去生成多面体的顶点,数量级会仍然发生几何级的膨胀。例如立方体有6个面,却有8个顶点;更一般地,p维立方体有2*p个超平面,却有2^p个顶点。
如果我们可以直接用多面体的超平面(facets)来表示linear inequality的话,可以进一步减少系统的复杂度。这就是我们用Farkas Lemma相比于Vertex Method能进一步获得的收益。
Farkas引理告诉我们:如果一个仿射函数在多面体的约束下总是非负的,那么该仿射函数可以用非负的系数和多面体约束(超平面)的线性组合进行表示,其中非负的系数称为Farkas因子。
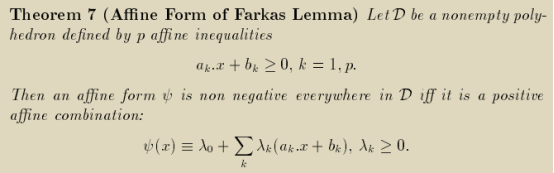
还是以第8小节的例子为例,θ1(i) =τ*i+α和θ2(i, j) =τ1*i+τ2*j+α的affine form分别在domain D1和D2上有函数值恒≥0的设定,应用Farkas引理,可以将原仿射函数写成Farkas因子和Domain上约束的线性组合的形式来进行表示。
如下所示,D1的约束有2个,D2的约束有4个,μ是非负的Farkas因子。
此时我们得到了一个新的跟原调度函数原型θ等价的表示,来替代原先未知系数是τ和α的函数原型。原先的τ和α的求解也不用再关心,现在我们的求解目标是μ。

十、动态依赖图<Ω, Γ>的描述方法:依赖多面体的定义
我们在第9小节中已经看到了operations的集合Ω(D1和D2的并集)是凸多面体(convex polyhedra),可以用多面体facets上约束的交集来表示。
同样地,依赖关系Γ也可以用多面体的形式来进行表示。

我们来解释一下上述定义的含义。如下图所示,对于<x, y>∈Γ(注意区分:<x, y>表示两个动态实例之间的依赖关系,e则对应<x, y>在PDG上抽象表示的静态语句之间的依赖边)、并且x∈DR、y∈DS,依赖多面体的维度是源点语句(σ(e))和汇点语句(δ(e))迭代空间的维度之和(维度p = pR + pS),且在依赖多面体中仍然包含DR和DS迭代空间的范围约束,另外还包含由procedence constraints关联起来的两个迭代空间上实例之间由依赖关系引入的等式约束。
可以理解成依赖多面体就是把依赖源点和汇点语句迭代空间给拼起来,并把存在依赖关系的实例用线给连起来,这些线的集合也是一个凸的多面体。
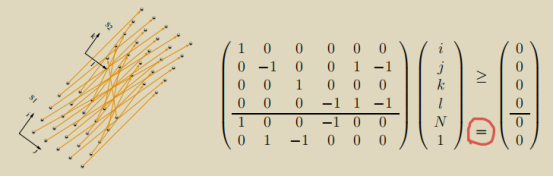

因为任何等式Ax=b都可以用两个不等式:Ax≤b和-Ax≤-b来表示,所以依赖关系中的等式部分也可以用多个不等式来表示。
并且,根据设定procedence constraints是仿射的,故依赖多面体中包含的所有不等式约束也都是仿射的,依赖多面体跟迭代空间一样,也是凸多面体(convex polyhedra)。
于是,同迭代空间的做法一样地,也可以对依赖多面体应用Farkas引理,compress由casuality condition包含的inequality,用依赖多面体的facets去抽象表示Γ所包含的所有依赖关系,简化系统的复杂度。
十一、举个栗子:依赖多面体的表示
如下所示,还是第8小节Figure 1的示例程序,我们之前在第9小节中刻画了迭代空间Ω的多面体表示,在这一小节里,我们继续刻画关于依赖关系Γ的多面体表示。
关于从语句S1(i’)->语句S2(i, j)关于数组元素s(i)的nonuniform Dataflow依赖,需要满足:i’= i ∩ j = 0。所以此时依赖多面体R1,2的维度是S1和S2的维度之和3(1+2),用3个迭代变量<i’, i, j>来表示,并且存在由procedence constraints关联起来的迭代变量之间的等式约束:i’= i ∩ j = 0;
同理,关于从语句S2(i’, j’)->语句S2(i, j)关于数组元素s(i)的uniform Dataflow依赖,存在4维的依赖多面体R2,2<i’, j’, i, j>,存在由procedence constraints关联起来的等式约束:i’= i ∩ j’= j - 1 ∩ j≥1。
并且还要把它们原始的源点语句和汇点语句的迭代空间中的约束也包含进来。

注:原始论文此处可能存在一些typo,所以我改了一下。
十二、一种简化的依赖多面体的表示方法
如果用一个仿射函数h(transformation function)去表示依赖关系中从汇点到源点的仿射映射关系,我们可以用一个维度同汇点语句迭代空间一样的依赖多面体Dσ(e)来替代Re,来降低依赖多面体Re的维度。

如下所示还是第11小节的例子,此时我们可以得到P1和P2,它们的维度跟依赖的汇点语句2的迭代空间的维度是相同的,是之前依赖多面体R1,2和R2,2的等价表示。
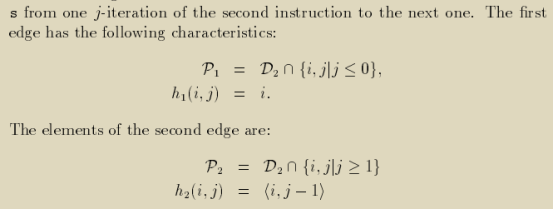
我们接下来会基于这种简化的依赖多面体表示法结合affine transformation function h,应用Farkas引理构建casuality condition的约束条件。
十三、关于最优化是否可以求到解的Decidability理论
注:因为本民科同学没有学过最优化和计算理论,本小节内容只能照本宣科一下。
最优化领域存在一种理论可以让我们在求解casuality condition的约束条件的时候判断出来是否能够求得最优解(Decidability OR Undecidability)。
对于求不到解的情形我们只能改设定或者换其他的方法了,幸运的是,我们多面体程序的迭代空间一般是有界的,nonuniform的依赖也不是无限的,不会立刻得出undeciable的结论,避开了定理4和5。
如下所示,可决性取决于两点:1)迭代空间是否是bounded的;2)依赖关系是否是uniform的。它们的组合与Decidable的关系如下所示。请大家自行体会,有懂的大佬麻烦教教我,谢谢大家。

十四、casuality condition约束条件的构建
现在我们继续从第12小节的结尾处开始,根据第9小节中得到的调度函数θ的原型(蓝框),和第12小节Dataflow Analysis得到的依赖多面体(紫框),来继续应用Farkas引理构建casuality condition的约束条件(红框)。

对照Farkas引理可见:由casuality condition构造的仿射函数Δe(y)就对应Farkas引理中在定义域恒≥0的仿射函数Ψ(x),Δe(y)函数的定义域就是依赖多面体P1和P2。
我们为程序中存在的每一个静态的依赖边都要应用一次Farkas引理,这需要代入不同的函数θ原型和相应依赖多面体的边界条件。

对于依赖边1:语句1->语句2,我们为Δe代入θ1和θ2的原型,并在依赖多面体P1上应用Farkas引理,得到以下等式。
注意其中λ是本次应用Farkas引理时引入的Farkas因子,μ是之前构造调度函数θ原型时应用Farkas引理时引入的Farkas因子,μ是我们待求的,而λ是我们希望消去的。
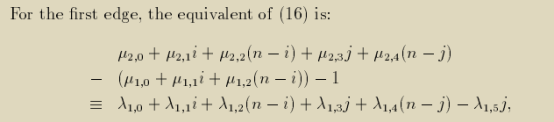
我们整理该等式,令等式两边所有相同的自由变量(包括迭代变量和结构参数)的系数分别相等,得到以下多个等式需要同时成立,其中所有Farkas因子λ≥0。我们称此过程为identification process。
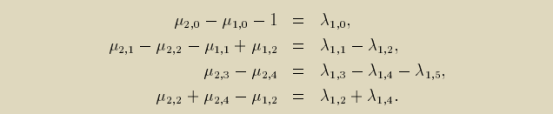
同理对于依赖边2:语句2->语句2,我们为Δe代入θ2和θ2的原型,并在依赖多面体P2上应用Farkas引理,也可以得到等式。
但是对于依赖的距离向量是常量的uniform依赖,我们也可以不必应用farkas引理而直接消去迭代变量(因为依赖的距离向量是常量),没有了迭代变量的Δe不存在infinite inequality进而不再需要应用Farkas引理去compress infinite inequality。
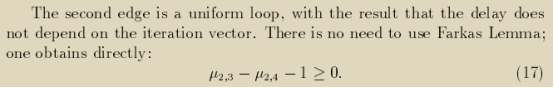
最终对于所有的依赖,这些等式和不等式的约束都需要同时成立,同时我们也可以尝试消去一些λ因子(也可以不消去)。整理的结果如下所示。
这些约束条件如果可以得到满足,那么casuality condition也都得到满足。——即,任意一组满足该约束的μ的解(λ是我们希望消去的),代入到第9小节的调度函数θ的原型中,都是一组满足casuality condition的调度函数。
接下来我们就需要从中选取一个特定解来优化某个人为设定的criterion,比如最小化执行延迟或者最大化系统吞吐率。
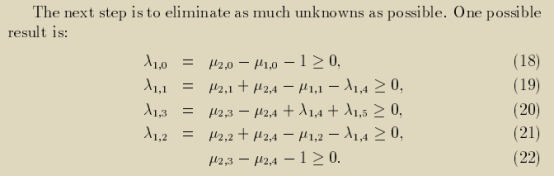
十五、casuality condition约束条件的计算机构建方法(with isl)
我们不难看到上述casuality condition约束条件的构建过程不过就是符号的代数运算,可以很容易地用计算机辅助我们进行运算。
可以用matlab或是sympy,我还是使用了我更熟悉的isl。因为涉及到了Farkas因子和迭代变量&结构参数的相乘,isl会认为这样的表达式不是仿射的,需要使用qpolynomial类。

现在我们再回过来看一下我们第6小节中举的另一个Figure 9的程序示例,我们当时说它没有一个一维时间的解可以同时满足系统中的两种依赖。这回我们就可以用我们编写的求解程序求得casuality condition约束条件(利刃在手杀心顿起!),并发现确实没有一组μ可以同时满足这两种依赖关系。

注1:本代码已push到:https://github.com/zhaosiying12138/isl/tree/autovec,欢迎大家来玩儿~~
注2:之所以是autovec分支是因为我懒得切branch了,我觉得写代码这种事有时候糊弄糊弄差不多就行了,,,
注3:本代码是半自动化求解,有的时候需要脑补,正如我一直所说的,本民科确实不太擅长写代码,,,
十六、casuality condition约束条件构建的正式表述
我们之前在第14小节中只是举了一个例子来介绍casuality condition约束条件的构造方法,下面我们用数学公式正式地再描述一遍。
式子(11)是迭代空间的约束,由implicit positive constraints调度函数θ≥0,对其应用Farkas引理得到调度函数θ的原型(14);
将式子(14)代入到casuality condition中得到式子(15);
式子(13)是简化了的依赖多面体的约束,依赖多面体上的表达式(15)Δe≥0,对其应用Farkas引理得到casuality condition约束条件的等价约束式子(16);
所有满足式子(16)的μ值代入到调度函数θ的原型都满足casuality condition的约束条件。
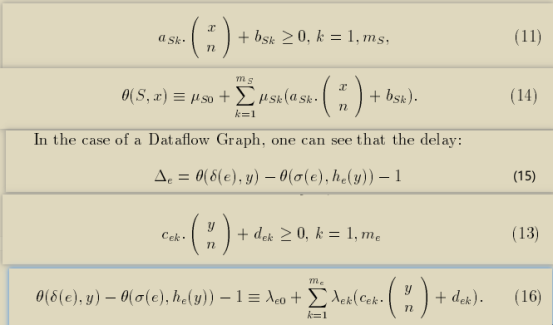
另外,应用Farkas引理的premise一定要确保定义域非空,需要保证迭代空间是非空的,以及用传统的依赖分析的方法判断出依赖多面体也是非空的。

十七、关于待求解系统复杂度的评估
在求解约束系统的最优解之前我们不妨先了解一下当前系统的复杂程度。
1. 该系统的未知系数由分别应用两次Farkas引理所引入的Farkas因子μ和λ组成。
对于每一个迭代空间DS,都会应用一次Farkas引理引入一组(ms+1)个Farkas因子μ,其中ms是该迭代空间DS内约束条件的个数,迭代空间的数量取决于程序中静态语句的个数Card V;
对于每一类由PDG抽象所表示的静态的依赖关系e,也都会应用一次Farkas引理引入一组(me+1)个Farkas因子λ,其中me是该依赖关系e对应的依赖多面体Pe内约束条件的个数,PDG上静态的依赖关系的数量是Card E。
最终系统未知系数X的数量是二者的加和。

2. 对于由每一个静态的依赖关系e应用Farkas引理得到的等式进行identification process令等式左右两边自由变量的系数分别相等可以得到(pδ(e) + |n| + 1)个等式。
其中pδ(e)是依赖关系汇点对应语句的迭代空间内迭代变量的个数,δ(e)表示一个静态的语句,也就是PDG上的Vertex,ps表示语句s迭代空间内迭代变量的个数;
|n|是identification process中等式内结构变量的个数,还要再+1是指等式左右两边的常量也要相等。
PDG上静态的依赖关系的数量是Card E。
最终系统包含的等式的数量是上述的加和。

3. 我们想探究X和Q的关系。
从实证的角度来说,对于任意一个语句,它对应的迭代空间上的约束条件的数量ms是迭代变量ps的2倍(例如:0≤i≤N,一个迭代变量有一个上界和一个下界共两个约束条件);
据作者所述,还是从实证的角度来说(机器学习-监督学习),对于一个依赖关系e,它对应的依赖多面体包含的约束条件的数量me是依赖多面体内语句的数量pδ(e)的2倍再加1。

代入以上两点的empirical facts,最终整理得到的X和Q的关系如下所示。
我们可以发现系统未知系数的个数X大约是系统中等式的个数Q的两倍。——即,该系统存在很多很多可行解,我们需要设定一个criterion来选取优化的解。

注(民科的找茬):我经过推导认为论文中该公式有误,所以进行了修改,但并不影响作者得出的结论。
另外我们可以还应用Gauss-Jordan消去法,结合Farkas因子≥0的约束,利用等式消去我们不需要的λ因子,将等式转变为一个不等式,从系统X个未知的系数中消去Q个未知的λ因子(if possible)。

正如第14小节结尾部分那样的,我们最终就用这种方法消去了Farkas因子λ1,0、λ1,1、λ1,3和λ1,2。
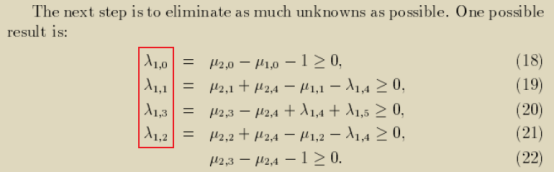
十八、Criterion之一:最小化调度延迟
我们之前在第14小节结尾的部分已经构建了为满足casuality condition系统需要包含的约束,在第17小节的分析中也可以看到该系统的未知系数远多于约束的数量,有很多解。下面我们需要人为devise一个criterion作为优化目标,使得既可以容易地求得解,得到的调度也可以使得程序的性能得到很好的并行优化。
最小化调度延迟的Criterion旨于最小化θ(u)的值,其中u∈Ω。
可以这样做的启发在于:在一个bounded的迭代空间中,仿射θ(u)会受限于一个结构参数n的仿射形式:L = h * n + k。于是对于在DS上,仿射函数:L - θ(u)≥0恒成立,
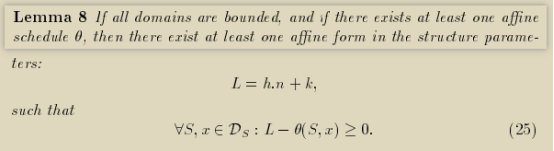
于是我们第三次应用Farkas引理,引入的farkas因子此时是υ,也是待消去的。
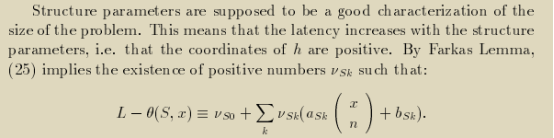
把新增的约束添加到原先在第14小节结尾处已经得到的满足casuality condition系统需要包含的约束中,对于这个充满了约束的多面体我们求解其lexicographic minimum的点,并赋予h和k最大的权重,更小的h和k意味着θ(u)被一个相对于结构参数n渐进(asymptotic)更小的L值所bounded。

十九、Criterion之二:受限的调度延迟
相比于Criterion 1优化整个系统最终完成的时间,Criterion 2试图优化依赖边的延迟(the delay associated to edge),使得任意存在依赖的两个operations之间执行的间隔时间不会超过一个常数δ。
虽然Criterion 1可以使得系统整体的性能很好,Criterion 2却可以更好地保证系统的公平性,使得系统中所有依赖的延迟都被限制在一个常数范围内,而与系统的执行规模Card Ω无关。
存在lifespan常数上限的依赖的程序也可以定期释放依赖源点存在数据传递的内存空间。
并且,在unbounded迭代空间的系统中此方法也可以求得最优解。
相比于蓝框的casuality condition,红框的Criterion 2有着类似的形式。同样我们可以类似于第18小节Criterion 1的求解方法,第三次应用Farkas引理,将约束添加进系统原有的约束中,然后赋予δ最大的权重,去求解多面体lexicographic minimum的点。

二十、类比 & 融会贯通——PLUTO变换算法中的Cost Function(选读)
注:本小节对比了Criterion 1 & 2和PLUTO循环变换算法设定的异同,不熟悉的小伙伴可以跳过,不影响Feautrier算法的理解。
学过PLUTO变换算法的小伙伴会发现其为数不多跟Feautrier调度算法不一样的设定(为数不多的创新点)就是cost function,但对比发现它的形式跟Criterion 2的delay schedule是一样的。

然后它又类似于Criterion 1,PLUTO赋予其一个仿射于结构参数n的上限,并应用Farkas引理求解。
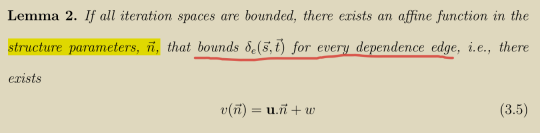
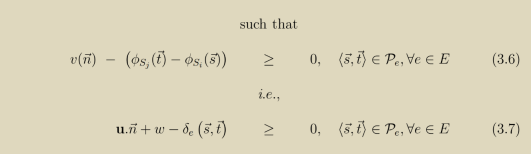

从数学的角度PLUTO的这种创新简直就是Criterion 1和2的缝合怪!尽管这里cost function在物理含义上可能更有深意,但用到的数学工具历经了16年也没有任何改进。
二十一、Criterion之三:为每个operation求调度θ的最小值
我之前在《零基础入门PLUTO的自动循环变换算法》一文中已经完整第展示了PLUTO循环变换的求解过程,当然也包括通过Cost Function的仿射约束应用Farkas引理得到的新的约束附加到系统已有约束并求解的过程。而且在上一小节中我也展示了Feautrier调度算法的Criterion 1和2的设定跟PLUTO的Cost Function从数学的角度上没有任何区别——
所以Criterion 1和2的编程的求解我这里就不演示了!感兴趣的同学可以阅读我PLUTO的文章。(本民科同学确实不太喜欢写代码,,,)
——不过!!Criterion 3的求解是一种全新的方法,本座还是亲自会演示一遍的!
Criterion 3基于一个定理:如果存在θ1和θ2都是满足casuality condition合法的仿射调度函数,那么θ3 = min(θ1, θ2)也是满足casuality condition合法的仿射调度函数,并且θ3的min operation是线性的,也不会破坏调度函数的仿射性。

为此,我们第14小节结束时已经得到的满足casuality condition约束的系统中,为Ω上每个operation都赋予调度函数θ满足约束条件下可以取到的最小的函数值,然后得到作用于整个Ω上的调度函数θ。

如式子(29)所示,我们的求解目标是在仿射函数原型的基础上为迭代空间上所有实例求它可以取到的最小的函数值。式子(28)即为我们之前得到的所有casuality condition约束。还需要包含有所有Farkas因子μ和λ≥0的约束条件。

然而该优化目标(29)涉及Farkas因子μ和自由变量x和n乘积的二次项,无法使用线性规划的方法进行求解。所以我们还需要应用线性规划的对偶定理,将优化的目标转换成仿射的形式再进行求解。
二十二、Criterion 3的求解:应用Linear Programming Duality Theorem
如下所示是线性规划的对偶定理,本民科只会用,不会证,请大家理解一下。
我们还是对Figure 1中的例子先试一下该定理应用的效果,然后再进行总结。
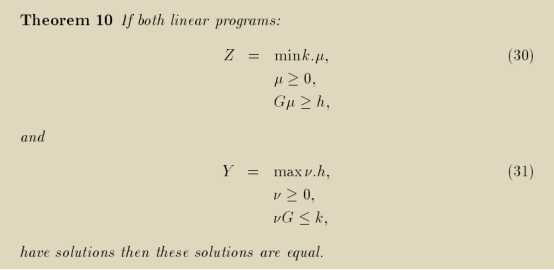
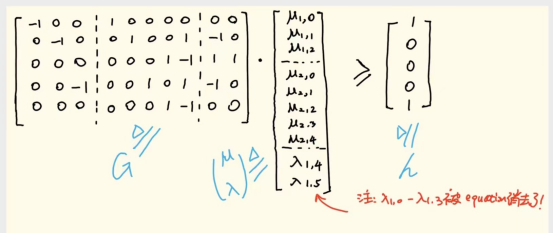
如下所示,对于在第14小节结尾处已经求得的约束系统(18)-(22)式,用(28)式的形式进行改写,得到如下形式。(感谢华为Matepad 11.5柔光版+二代手写笔提供的技术支持,遥遥领先!)

下面是我们在第9小节中已经得到的两个语句对应的调度函数的原型,(29)式要对它们分别求最小值。
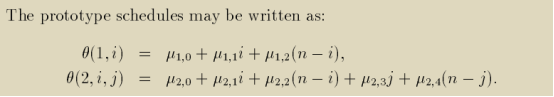
我们将(29)式经过整理用(30)式的形式进行表示,再根据线性规划的对偶定理,(30)式和(31)式是等价的,于是将(29)式转换成(31)式进行表示。
对于语句1有:
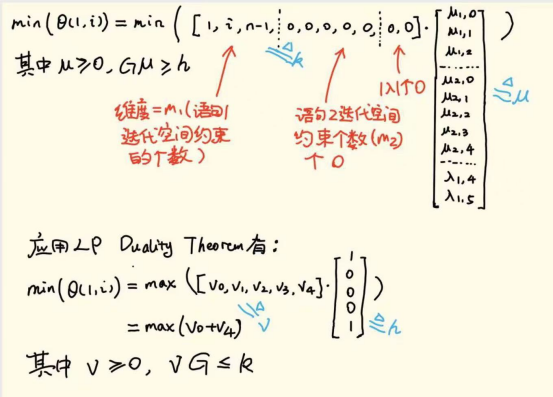

对于语句2有:

这样变换的好处在于:转换后(31)式的优化目标函数max(v * h)变为仿射的了,并且把原先优化目标函数中的包含自由变量的k向量转移到现在的约束v * G≤k中了。——即,现在的约束是参数化的(parametric),但可以用parametric linear programming程序进行求解。
现在我们分别将两个语句对应的优化目标函数(v0 + v4)和约束传给isl工具进行lexicographic maximum求解,得到一个参数化的解。
P1 := [i, n] -> {[result, v0, v1, v2, v3, v4, i, n] : result = v0 + v4 and v0 >= 0 and v1 >= 0 and v2 >= 0 and v3 >= 0 and v4 >= 0 and i >= 0 and n - i >= 0 and -v0 <= 1 and -v1 <= i and -v3 <= n - i and v0 <= 0 and v1 <= 0 and v3 <= 0 and v2 + v4 <= 0 and v1 - v2 + v3 - v4 <= 0 and -v1 + v2 - v3 <= 0 and v3 <= 0};
lexmax P1;
P2 := [i, j, n] -> {[result, v0, v1, v2, v3, v4, i, n] : result = v0 + v4 and v0 >= 0 and v1 >= 0 and v2 >= 0 and v3 >= 0 and v4 >= 0 and i >= 0 and n - i >= 0 and j >= 0 and n - j >= 0 and -v0 <= 0 and -v1 <= 0 and -v3 <= 0 and v0 <= 1 and v1 <= i and v3 <= n - i and v2 + v4 <= j and v1 - v2 + v3 - v4 <= n - j and -v1 + v2 - v3 <= 0 and v3 <= 0};
lexmax P2;

验证求得的解跟论文的解是一致的。
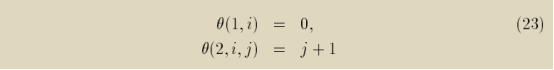
最后根据此调度进行代码生成,得到以下变形后的程序。

上述求解过程更正式的表述如下所示,大家可以对照着之前手写的求解示例来看,在此就不再过多赘述了。

二十三、Criterion 3求得的解是一个分段函数
如第21小节的式子(27)所示,Criterion 3求得的解是一个分段函数。上一小节中求得的解不是分段函数是它运气好(也可能是运气不好),那么我们下面再举一个例子。
考虑以下recurrence equation的程序示例。

交由isl工具进行最优化求解得到分段函数,有3个解对迭代空间进行了划分,其中每个subdomain对应特定的调度函数,该函数在该subdomain下是最优的。下面截图中的下划线表示subdomain的范围,矩形框表示特定的调度函数,对比论文中给出的结果,是一致的。
P1 := [j1, j2, s] -> {[t, u, v, j1, j2, s] : t = u + v and u >= 0 and v >= 0 and j1 >= 0 and j2 >= 0 and j1 + j2 - s >= 0 and 2s - j1 - j2 >= 0 and 2u <= j1 and 2u + 3v <= j2 and 4u + 3v <= j1 + j2 - s and -4u - 3v <= 2s - j1 -j2 };
P2 := {[t, u, v, j1, j2, s] -> [t]};
coalesce(range(P2 * lexmax(P1)));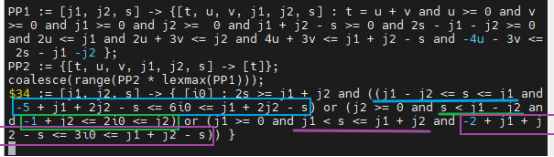

注:紫色下划线中j1 < s≤j1+j2的条件跟论文中j2 - j1 + s≥0 ∩ j1 < s的条件是等价的。
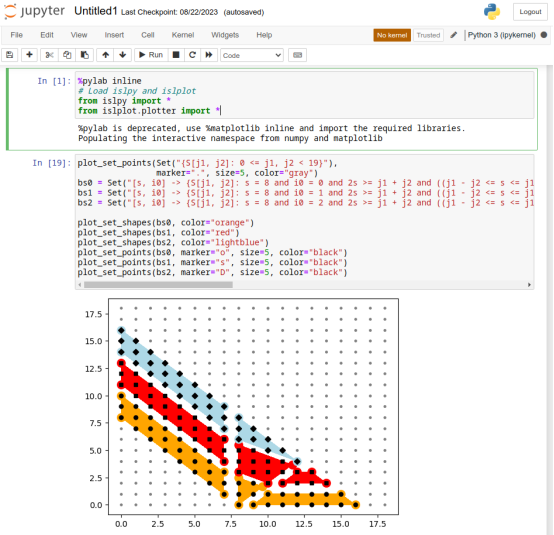
然后我们设定s = 9跟论文中的设定保持一致,使用islplot工具[6]画出调度值θ分别等于0, 1, 2时对迭代空间的划分。我们只需要把刚才isl输出的结果,结合我们对结构参数的设定,再喂给islplot绘制出集合覆盖的区域和内部包含的整数点即可。
jupyter notebook .
%pylab inline
# Load islpy and islplot
from islpy import *
from islplot.plotter import *
plot_set_points(Set("{S[j1, j2]: 0 <= j1, j2 < 19}"), marker=".", size=5, color="gray")
bs0 = Set("[s, i0] -> {S[j1, j2]: s = 8 and i0 = 0 and 2s >= j1 + j2 and ((j1 - j2 <= s <= j1 and -5 + j1 + 2j2 - s <= 6i0 <= j1 + 2j2 - s) or (j2 >= 0 and s < j1 - j2 and -1 + j2 <= 2i0 <= j2) or (j1 >= 0 and j1 < s <= j1 + j2 and -2 + j1 + j2 - s <= 3i0 <= j1 + j2 - s)) }")
bs1 = Set("[s, i0] -> {S[j1, j2]: s = 8 and i0 = 1 and 2s >= j1 + j2 and ((j1 - j2 <= s <= j1 and -5 + j1 + 2j2 - s <= 6i0 <= j1 + 2j2 - s) or (j2 >= 0 and s < j1 - j2 and -1 + j2 <= 2i0 <= j2) or (j1 >= 0 and j1 < s <= j1 + j2 and -2 + j1 + j2 - s <= 3i0 <= j1 + j2 - s)) }")
bs2 = Set("[s, i0] -> {S[j1, j2]: s = 8 and i0 = 2 and 2s >= j1 + j2 and ((j1 - j2 <= s <= j1 and -5 + j1 + 2j2 - s <= 6i0 <= j1 + 2j2 - s) or (j2 >= 0 and s < j1 - j2 and -1 + j2 <= 2i0 <= j2) or (j1 >= 0 and j1 < s <= j1 + j2 and -2 + j1 + j2 - s <= 3i0 <= j1 + j2 - s)) }")
plot_set_shapes(bs0, color="orange")
plot_set_shapes(bs1, color="red")
plot_set_shapes(bs2, color="lightblue")
plot_set_points(bs0, marker="o", size=5, color="black")
plot_set_points(bs1, marker="s", size=5, color="black")
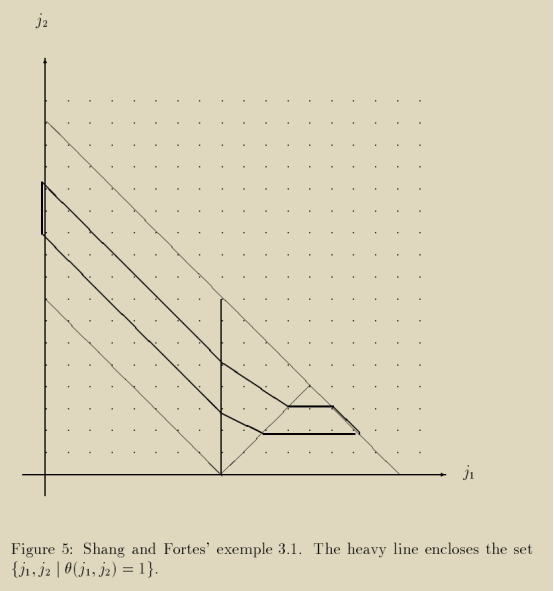
plot_set_points(bs2, marker="D", size=5, color="black")最终我们复刻出了跟论文图例一样的分段函数表示。
二十四、Criterion 3的解包含Criterion 1的解,具有最小的调度延迟
Criterion 1的解θL是有效的,它一定包含在集族G中。
Criterion 3从集族G中为每个operation选取调度值最小的点,组成θmin,则θmin不会差于θL。
θL又是已知可以得到的具有最小调度延迟的解,θmin在这一方面也不会超过θL。
故综上,Criterion 3求得的解也具有最小的调度延迟,并在其他操作上可能优于θL的解。——即,在Criterion 3中虽然我们没有像在Criterion 1中为θL设置一个仿射于结构参数的上界,我们也同样用不同的方法求出了满足Criterion 1的解,甚至在其他方面还可能优于它。殊途同归。
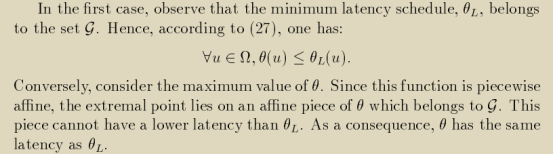
二十五、总结:把大象塞冰箱里总共分三步
1)根据迭代空间多面体构建仿射调度函数θ的原型;
2)根据依赖多面体继续构建满足所有casuality condition约束条件的调度函数θ的约束条件;
3)将取到约束条件下每一个操作能取得的调度函数的最小值作为调度函数θ的优化目标,应用线性规划的对偶定理求解出关于函数原型未知参数的解,这是一个分段的仿射函数,并且具有最小的调度延迟。(前篇完)
二十六、参考文献
[1] Feautrier P. Some efficient solutions to the affine scheduling problem. I. One-dimensional time[J]. International journal of parallel programming, 1992, 21: 313-347.
[2] Bondhugula, Uday Kumar. Effective automatic parallelization and locality optimization using the polyhedral model. Diss. The Ohio State University, 2008.
[3] Griebl, Martin. Automatic parallelization of loop programs for distributed memory architectures. Passau, Germany: Univ. Passau, 2004.
[4] Shang W, Fortes J A B. Time optimal linear schedules for algorithms with uniform dependencies[J]. IEEE Transactions on Computers, 1991, 40(06): 723-742.
[5] Paffenholz A. Polyhedral geometry and linear optimization[J]. Technische Universität Darmstadt, 2010.

