allenlu2007

Linear quadratic regulator (LQR) 包含兩部份：linear dynamic system 和 quadratic cost (u) and regulator (x) function.    LQR 可以說是最基本而且使用廣泛的 optimal controller.  即使 real dynamic system and cost function 並非 LQR, 在 linearized 之後 local region 也可用 LQR approximation.

LQR Problem Formulation

Quadratic cost function with final cost (Sf term)  and x ∈ ℜ^n , u ∈ ℜ^m:

Subject to the linear first-order dynamic constraint

and the initial condition

 或如下相同的定義

Optimal control 的目標是 keep x(t) 儘可能接近 0, 特別是在 tf 時, 同時用越小的 u(t) (能量) 越好。

* x’ Sf x penalizes final state deviation.  

* x’ Q x penalizes the transient state deviation.  

* u’ R u penalizes control effort. 

 

幾種 LQR 變形:  

* A, B, Q, R 是 time varying or time invariant

* Cost function:  是否含 final cost (Sf term), and time horizon (t0 and tf); 是否含 cross term; 是否有 discount function

* 是否有 separate 的 output state y(t) = C(t)x(t).  

 

先考慮基本型: time-invariant ABQR, finite and fixed horizon with final cost

 

 

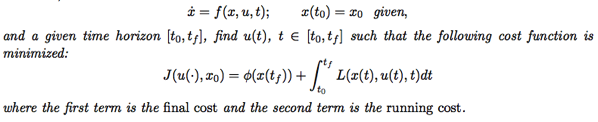
Hamiltonian and Solution

The control Hamiltonian 

H(x, λ, u, t)  = λ f(x, u, t) + L(x, u, t)

   

以及相關方程式:

dλ/dt = –∇xH = –∂L/∂x – λ ∂f/∂x  = -Q x – A λ

dx/dt = ∇λH = f(x, u, t) = A x + B u

∇uH = λ ∂f/∂u + ∂L/∂u = 0 = B λ + R u

 

和 Boundary conditions

x(to) = xo

λ(tf) = ∂𝜙(x(tf))/∂x

 

In summary

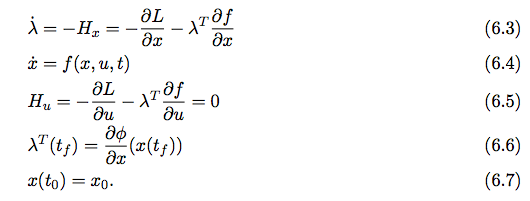
Proof and solution 見 reference.

 

Solution 分為 open loop and close loop solutions

是否可用圖解?  比較 Kalman filter 和 HMM 的 graph model???

 

先是 open loop solution:   u(t) = -R^-1(t) B'(t) λ(t)

 

以上是 open loop solution,  可以把 u(t) 乘上 gain (K(t)) 負回授到 x(t) 成為 close loop

close loop solution 如下:

λ(t) = P(t) x(t)    P(t) 是 Riccati Differential Equation (RDE) 的 solution

u(t) = -R^-1(t) B'(t) λ(t) = -R^-1(t) B'(t) P(t) x(t) = -K(t) x(t)  where K(t) = R^-1(t) B'(t) P(t)

 

Theorem 6.2.2 的最小值 J* = xo’ P(xo) xo, 乍看只和初始值 xo 相關?!  No, 其實不然。雖然  xo 是 given initial value.  P(t) 則和 final cost 的 S 以及 CTRDE 相關 (見 6.13).  所以 P(xo) 和 final cost x(tf)’ S x(tf) 相關。 一個觀察是 to 接近 tf 時，最小值 J* = x(tf)’ S x(tf) = x(tf)’ P(tf) x(tf)  where P(tf) = S as expected.

The control formulation works for time varying systems, e.g. nonlinear systems linearized about a trajectory.

 

似乎 open loop:  (6.8), (6.9), and (6.10)

而 close loop: (6.12), and (6.13).  兩者並非完全等價 (?)，實務上以 close loop 為主。

 

What is λ(t) and P(t)? Costate Relation and Cost-to-go function

λ(t) 是 x(t) 的 costate (x(t) 是 state).  也是 Lagrange multiplier 的 coefficient.  前文提到這個 coefficient 對應 Lagrangian 和 constraint functions 的 normal direction parallel 的 scaling factor. 

 

λ(t) sort of 對應 Hamiltonian mechanics 時的 p(t), generalized momentum.  或是 Legendre transform 的 p (斜率).   Lagrange multiplier 的 λ 和 Legendre transform 的 p 似乎有強相關???

 

λ(t) = P(t) x(t)    P(t) 是 Riccati Differential Equation (RDE) 的 solution

P(t) = λ(t)/x(t) where λ(t) is the costate, x(t) is the state.  P(t) 是一個比例 scaling matrix.

在 transient state 時 P(t) 是 time-varying; 在 steady-state 時 P(t) 會收歛到一個 fixed matrix.

 

P(t) 另一個意義是 cost-to-go function.   

對於任何 t 介於 [to, tf],  對於剩餘 [t, tf] 的滿足 (6.1) and (6.2) 的最小值 J*(u, x(t), t, tf) = x(t)’ P(t) x(t).

因此 P(t) 也被稱為 cost-to-go function, 事實上光 P(t) 還不夠，需要 x(t) (initial condition at t) 才能算出真正的 cost-to-go.  下一個問題是如何得到 x(t)?  It turns out 在 LQR control 中，x(t) = Φ(t, to)xo where Φ(t, to) is the transition matrix for A(t)-B(t)K(t) (意即 exp[A(t)-B(t)K(t)]).  當然 K(t) depends on P(t), 需要解 CTRDE 才能得到。

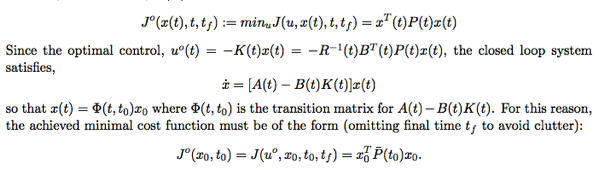
更多關於 P(t), sub-interval optimal, 以及和 dynamic programming, discrete LQR, and Bellman equation 的關係請見另文。 

 

再先考慮簡單型: time-invariant ABQR, infinite horizon (without final cost)

All matrices (i.e., A, B, Q, R) are constant, the initial time is arbitrarily set to zero, and the terminal time is taken in the limit  (infinite horizon).  Infinite horizon 隱含 zero terminal cost (why?)

 

Minimize the infinite horizon quadratic continuous-time cost functional

Subject to the linear time-invariant first-order dynamic constraints

and the initial condition

 

Solution

It has been shown in classical optimal control theory that the LQ (or LQR) optimal control has the feedback form

where  is a properly dimensioned matrix, given as

and  is the solution of the differential Riccati equation. The differential Riccati equation is given as

For the infinite horizon LQR problem, the differential Riccati equation 在 steady state is replaced with the algebraic Riccati equation (ARE) given as

Time-invariant system, infinite horizon (no terminal cost), with cross term

Solution

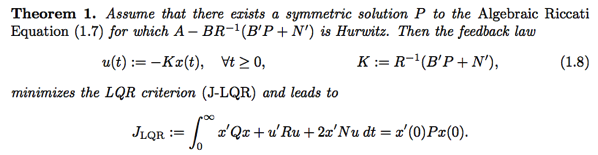
和 no cross term 相比多了 N.  如果 N=0 則化簡為基本型。P 是 costate 嗎? 

No, almost,  costate p(t) = P x(t).

 

Feedback System and Close Loop Dynamics

以上 optimal control 的 solution  u(t) = -K(t) x(t) 可視為 feedback control loop.  原來的 linear dynamic system 可以化簡如下。最終的 close loop response 變成 n 個 1st order differential equations.  

 

Control Hamiltonian

 H(p, x, u, t) = fp + F = (Ax + Bu)p + 1/2 (x’Qx + u’Ru) 

dH/dp = Ax + Bu = dx/dt 

dH/dx = Qx + Ap = -dp/dt

dH/du = Bp + Ru = 0

如果把 u = -(R^-1)B’p 得到以下 equations:

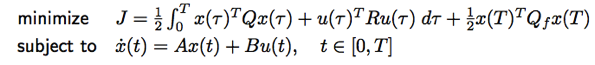
  上述 λ(t) 就是 costate (之前我們用 p(t)) 

 

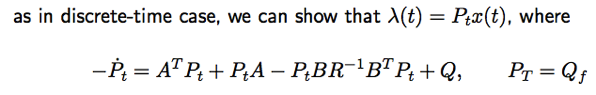
Costate: p(t) = λ(t) = Pt x(t)        

Optimal control: u(t) = -R^(-1)B’ λ(t) = -R^(-1)B’ Pt x(t) = – Kt x(t) ==> Kt = R^(-1) B’ Pt 

x(t) 如上述 close loop dynamics 是 n 個 1st order differential equations solution (exponential functions).

p(t) 和 u(t) 則是 x(t) components 的 linear combinations.

 

Hamiltonian Matrix 是什麼

Hamiltonian matrix 好像和 control Hamiltonian 沒有麼關係? 

[ p(t)  I(t)] H [ x(t) ? ] =  fp + F = (Ax + Bu)p + 1/2 (x’Qx + u’Ru)  (?)

 

Hamiltonian Matrix and ARE

[P -I] H [I P]’ = 0  可以得到 ARE.

 

Hamiltonian Matrix Eigenvalues

Hamiltonian matrix 可以 linear 轉換成 upper triangular matrix 如下。得到 eigenvalues (2n) 和 close loop 一樣 (A+BK)。 Eigenvalues of Hamiltonian H are λ1, . . . , λn and −λ1, . . . , −λn

 

 

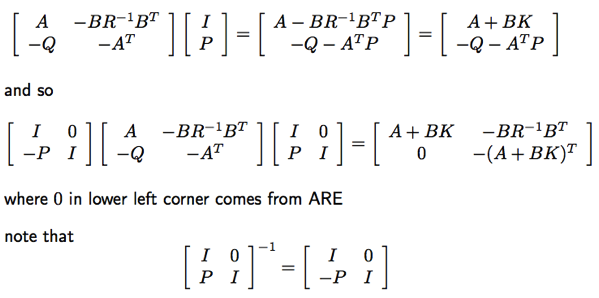
Further Study

Hamiltonian Matrix Phase Margin and Gain Margin 

Optimal control

discrete time LQR (Stanford 363): Bellman equation

Bang-bang controller

least time 

least fuel